*文章授权转自微信公众号「包小猩CG杂货店」
今天咱们来聊聊分形基础。分形这个名词或许你之前听说过,但是他具体是什么东西呢?别着急,接下来我会从分形的背景开始讲起,到分形的算法公式,以及经典的曼德勃罗集合和朱利亚集合。相信认真看完后你一定会有所收获。
一、分形的诞生
1967年,数学家 曼德勃罗(B.B.Mandelbrot)在美国权威的《科学》杂志上发表了一篇严谨的学术论文:《英国的海岸线有多长?统计自相似和分数维度》,如果单看文章标题你肯定觉得:这不就是个标题党嘛,英国海岸线有多长量一下不就出来了啊?但真的这么简单吗?其实事实并非如此,因为文章最后的结论表明:英国的海岸线长度是无法精确测量的!
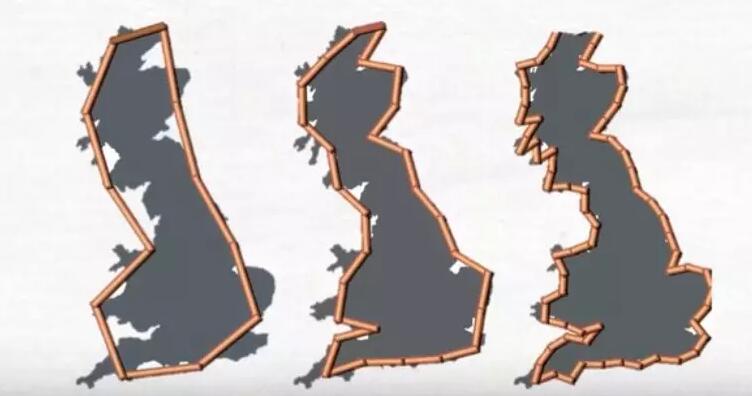
(图像:使用不同长度的测量尺测量英国海岸线)
这时你一定会对结果感到疑惑,为什么是无法精准测量的?在这里我找到了一张非常直观的图片,如上图所示,当我们用越来越小的尺子去测量英国海岸线的长度时,得到的结果将会越来越准确。所以海岸线的长度其实是和测量工具的尺寸挂钩的。当测量工具尺寸越小,得到的数值就越准确,相应的长度也会增加。所以如果你使用的测量工具无限小,英国的海岸线长度将会趋于无限。乍听起来会觉得非常哲学,仿佛有限的世界中蕴藏着无限。
在这种思维下,分形就产生了。

(图像:Koch曲线)
关于分形本身,维基百科给出的定义是:“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都是整体缩小后的形状”。这说明分形本身就是一种不断自我迭代的过程,就好像上面英国海岸线一样,如果我们将所有建筑和参照物去掉,100公里的海岸线和10公里的海岸线形状是近似的,这也就是我们下面要说到的自相似性。在现实生活中我们可以发现很多分形现象的存在,比如鹦鹉螺的壳、罗马花椰菜还有雪花。所以使得数学构造上的分形,在艺术创作领域也有着一席之地。

(图像:鹦鹉螺壳)

(图像:罗马花椰菜)

(图像:雪花)
当然分形本身也具有很多特性,比如自相似性
自相似性通俗来说的意思就是无论以什么大小尺度来看分形的形状都是相似的。比如下图两张曼德勃罗集合分形图案,坐标放大的尺寸相差了接近100倍,但是他们看上去却是那么相似。所以我们可以说分形在常规的几何变换中是具有不变性的,即标度无关性


而且分形有个很好玩的特点,就是在数学上,他是处处不可微的(也可以说是处处不可导的)。因为分形本身就是一种无限迭代的过程。我们传统测量非分型曲线时候,如二次函数曲线,只要放大到足够大,总能用直线拟合一小段曲线,在一小段范围内取一阶泰勒展开,近似为直线,然后求和总长度。但分型曲线是不能这么做的,如果尝试使用直线去拟合分形曲线,如科赫雪花曲线,缩放的过程永远不会停止,因为分形图案是无限迭代的,无论缩放到多小,细节总会不断地出现。这种函数最典型的代表就是魏尔斯特拉斯函数,他的特性就是处处连续但处处不可导。
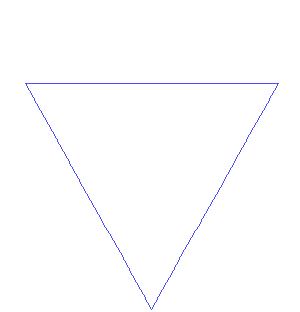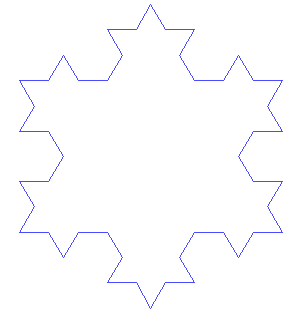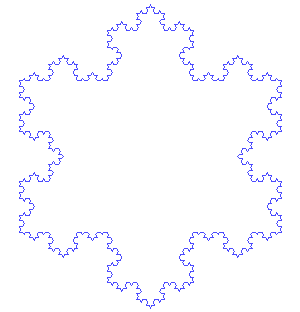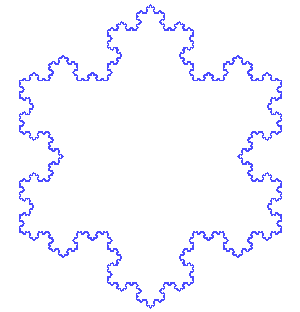
(图像:科赫雪花)
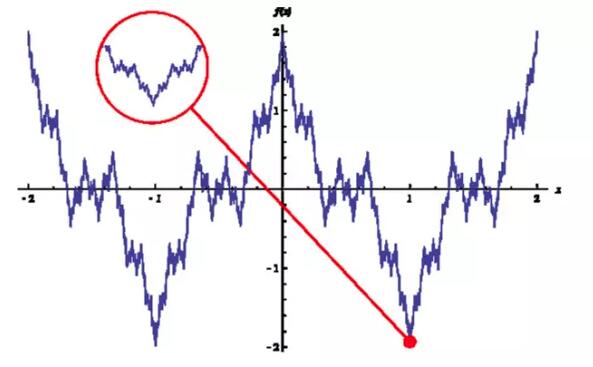
(图像:魏尔斯特拉斯函数)
二、分形的典型公式
通过上面的科普后我们知道分形具有自相似性,当然这也从另外的角度说明了分形是一种不断递归的算法。
所以接下来我们就可以请出大名鼎鼎的分形复变函数:
Z = Z² + C
乍一看你可能会觉得很懵,这个等式到底是什么意思,接下来请听我慢慢解释。
这是 曼德勃罗集合(Mandelbrot Set)和 朱利亚集合(Julia Set)都会用到的复变函数。这里 Z 和 C 都是复数。
简单科普一下复数的概念:复数由实部和虚部共同组成,实部为我们常见的实数,虚部就是虚数的集合,我们可以将其写成形如 z=a+bi(a,b均为实数)的表达式,其中a为实部,bi为虚部, z 当然就是复数。
复数的存在就说明基于 Z = Z² + C 的分形函数其实是二维的,因为他同时拥有实部和虚部两个维度,所以我们接下来就会在复平面(实部和虚部构成的二维平面,类似平面直角坐标系)上研究基于复变函数的两个经典集合。
值得注意的是,这里的等号其实是程序中的赋值,而递归的操作就是不断的将左边的 Z 带入右边的公式计算,得到一个新的 Z,这样多次迭代之后,Z 的值会出现很奇妙的变化,这与我们下面要讲到的曼德勃罗集合(Mandelbrot Set)和 朱利亚集合(Julia Set)有很大联系。
三、曼德勃罗集合
曼德勃罗集合虽然听起来很陌生,但是她的图像你一定见过,没错就是下面这张:

图像非常酷炫是不是!但是他是怎么得来的呢?
这里又要说到前面讲的这个公式了:Z = Z² + C
让我们一起来做个假设:假如我们取复平面上的任意一点 a,然后将复数 a 代入 C 中,从 Z=0 开始,不断迭代 Z = Z² + C ,这时候会出现什么情况呢?
为了让你们更加清楚这个计算过程,同时为了方便计算,我们暂时抛弃虚部,全部在实轴上取点代入复变函数计算。比如我们取点 a = -1 和 b = 1 ,代入复变函数迭代 10 次,看看会发生什么:
第一次:a=0²-1=-1 b=0²+1=1
第二次:a=(-1)²-1=0 b=1²+1=2
第三次:a=0²-1=-1 b=2²+1=5
第四次:a=(-1)²-1=0 b=5²+1=26
第五次:a=0²-1=-1 b=26²+1=676
第六次:a=(-1)²-1=0 b=676²+1=456977
第七次:a=0²-1=-1 b=456977²+1=208827978530
第八次:a=(-1)²-1=0 b=208827978530²+1=43609124616926140960901
第九次:a=0²-1=-1 b=.......啊写不下了
第十次:a=(-1)²-1=0 b=............BOOM!
可以看到经过10次迭代的洗礼之后,a点的值一直保持着稳定循环,而b点则直接指数爆炸了
当然在复平面中存在着无数这样的点,他们有些会像 a 点这样不断循环或收敛,有些则会像 b 点这样直接数值爆炸飞到天际。如果我们将a点的集合全部收集起来,就是曼德勃罗集合。图像中的黑色区域就是类似 a 点的所有复数的集合。而图像中的颜色代表不同位置的点逃离此区域所用的次数,亮度值越高表明逃离出去耗费的次数越多。

如果你有心将 Z= Z² + C 的图像画出来,在不同C的取值情况下这个二次函数会与y=x有非常奇妙的关系。(为什么是与y=x呢?因为这代表着一个极限,就是刚好落在集合边缘的值)
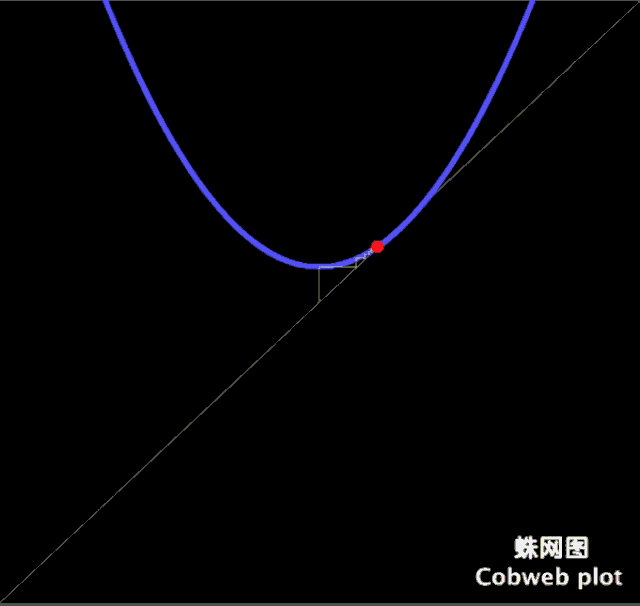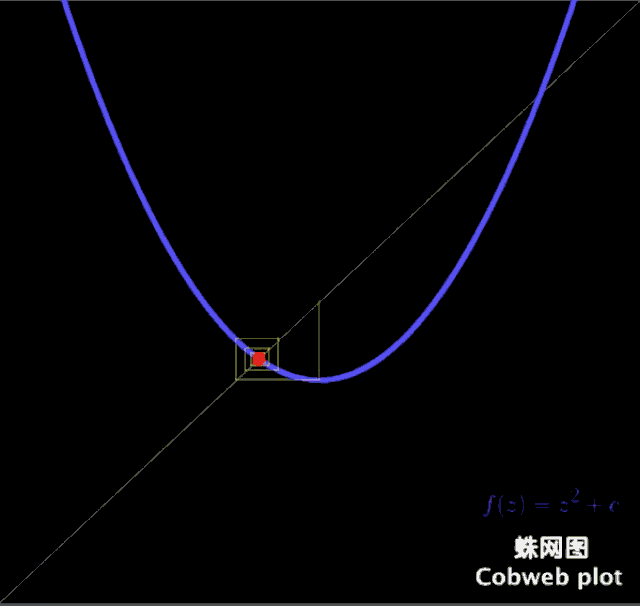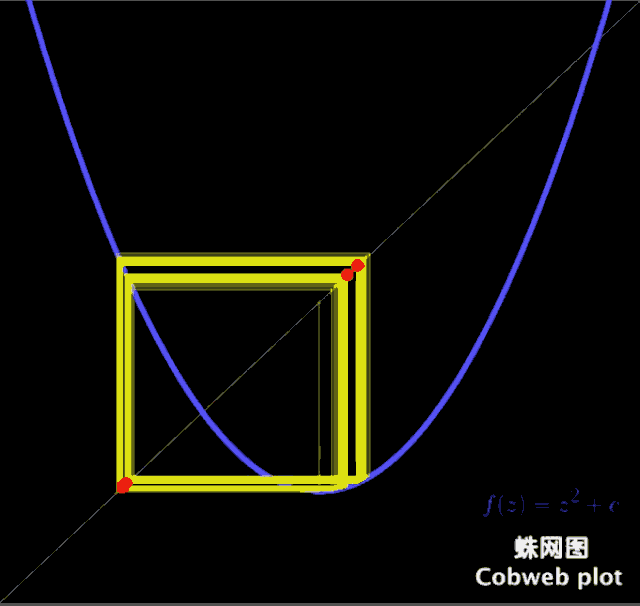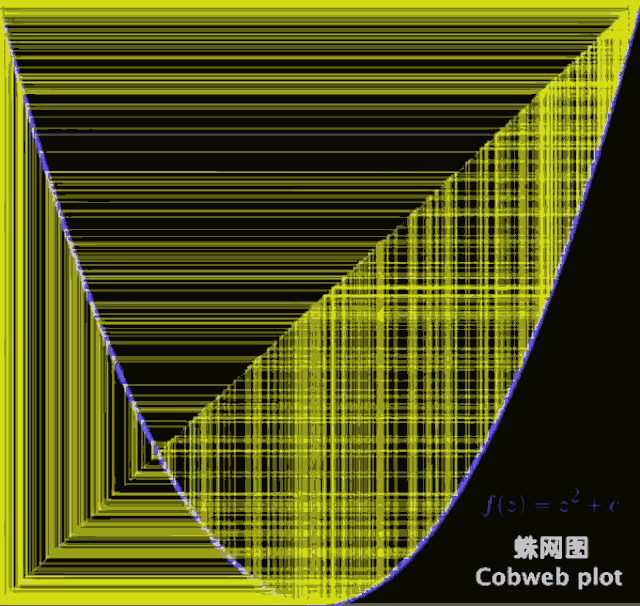
可以发现当c取-2的时候(也就是到达最底下的时候)所有取值都消失了,所以我们定义 Z= Z² + C 的边界为2,也就是在复数长度大于2的部分是不存在收敛值的。
四、朱利亚集合
朱利亚集合和曼德勃罗集合非常类似,他们都来自同样的复变函数,即 Z=Z²+C 。它与曼德勃罗集合不同的是:曼德勃罗集合是将复平面上的点赋予 C ,然后从 Z = 0 开始迭代。而朱利亚集合则是将复平面上的点赋予Z,然后将C赋予任意数开始迭代。
虽然咋一看好像二者差不多,但是就是这样小小的区别导致了二者函数图像的大不相同。同样也造成了两种集合的意义差别:曼德勃罗集合是从0点开始不断迭代复平面上的任意一点,观察是否收敛。而朱利亚集合则是实验复平面上的任意一点,观察是否收敛。
除此之外,朱利亚集合的其他部分和曼德勃罗集合基本上差不多,不过因为C 可以任意赋值,所以在改变 C 的取值后,我们可以得到这样动态的图像:
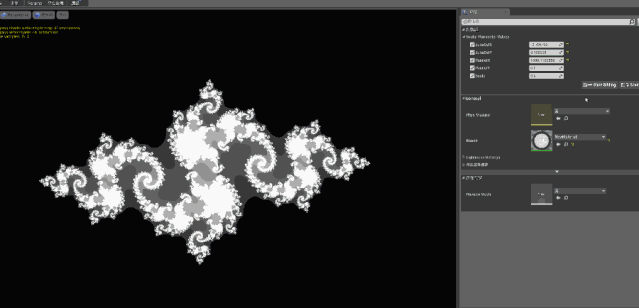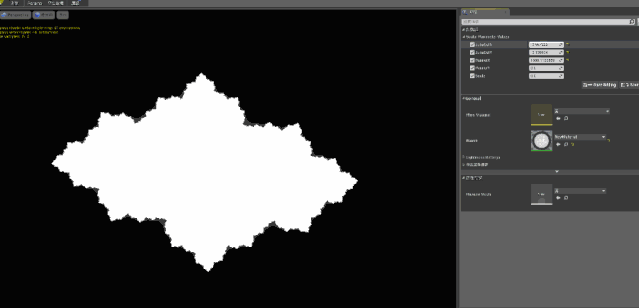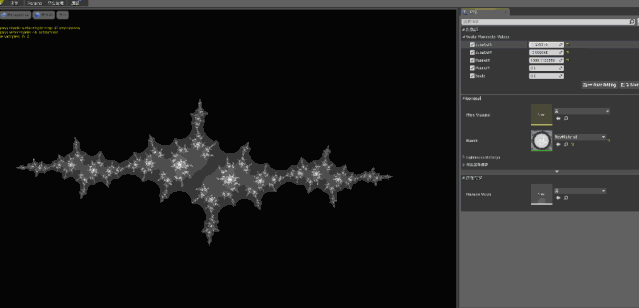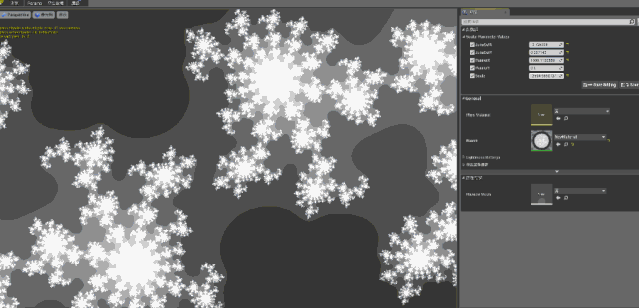
当然如果你问:既然朱利亚集合都能动,为什么曼德勃罗集合不能动呢?
其实告诉你,是可以的。我们只需要将复变函数改成 Z=Z^n+C 就好了,然后改变n即可改变曼德勃罗集合的形状。关于这部分在后续的实现章中有更加精彩的讲解,记得关注公众号得到第一时间推送哟。

到这里,分形基础讲解已经差不多完成,其实分形的基本概念非常简单,但是它和几何挂钩,简单的公式即可生成无限细节的复杂图案,其中的美妙不言而喻。
最后记得点赞收藏转发哟 ~~ 么么扎!
(本文部分配图来源于网络)
欢迎关注“包小猩CG杂货店”微信公号
