*文章授权转自微信公众号「包小猩CG杂货店」
这次来更新一下分形的上色。
咱们现在填坑的范围仅限于 2d 分形,如果后面有时间我会继续拓展到三维分形,任务艰巨可能会涉及到四元数等知识,希望我能填完吧咕咕咕。
好的说正题,关于上色,这篇文章主要分两部分讲解:一是如何使用色盘(Color Palattes)函数给灰度渐变映射上颜色。第二呢就是本次文章的重点了:如何插值平滑分形之间的过渡,让最终的图像呈现非常漂亮的颜色渐变效果。难点主要集中在第二部分,我也卡了一段时间才弄懂,或许聪明的你比我强很多,一遍看懂不成问题。既然来都来了,坚持看下去,你一定会有收获。话不多说开始今天的骚操作。
一、使用色盘(Color Palattes)映射颜色
在讲解映射颜色的做法之前,我先给大家说几个熟悉的东西。咱们都知道渐变色,很多软件中都可以生成。就是下图这个东西,我们可以任意加点实现颜色过渡的效果:

如果将渐变色和调色结合起来呢?经常用 ps 调色的朋友应该知道,在 ps 中有个工具叫渐变映射,作用就是根据原图亮度值的不同分配渐变中不同的颜色。sd 中也有这个工具,名字叫 Gradient Map(如下图所示,将左图按亮度映射渐变色得到右图的结果)。

可以看到,这种上色的方式效果不错同时易于控制,非常契合分形上色的需求(因为分形出来的结果也是黑白的灰度效果),于是我们选择这个方法给分形上色。
简单梳理一下,我们现在需要做两方面的工作:第一是做出色板,第二就是将色板运用到原始灰度上。
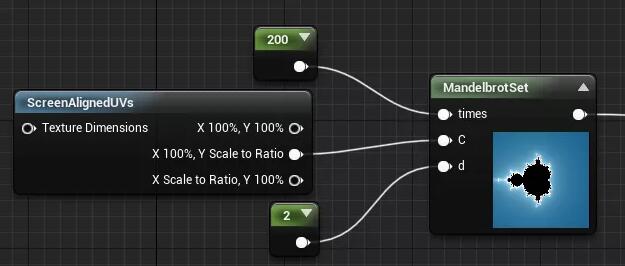
我用ue4做了套简单的节点来阐述色板的实现原理:
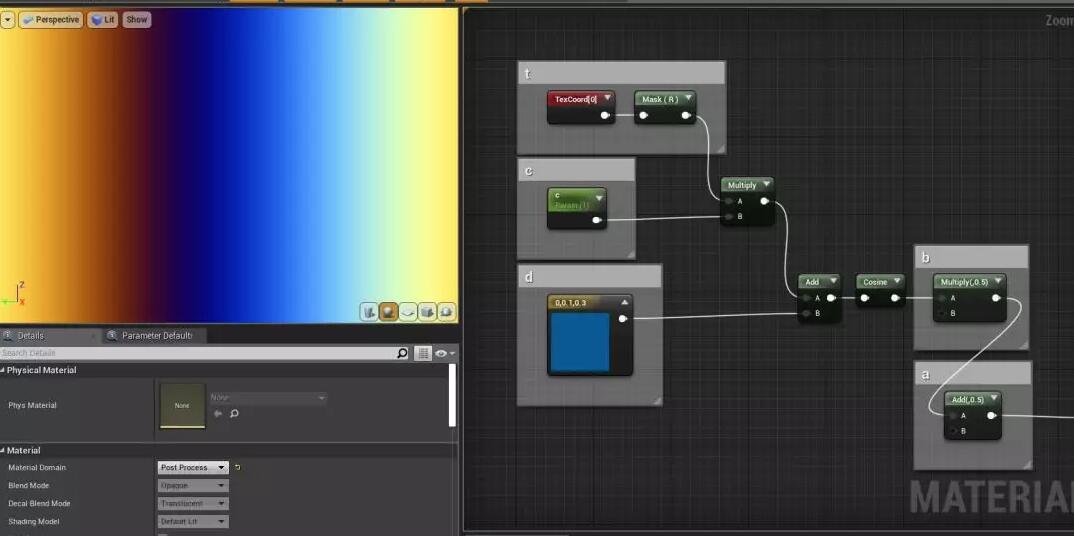
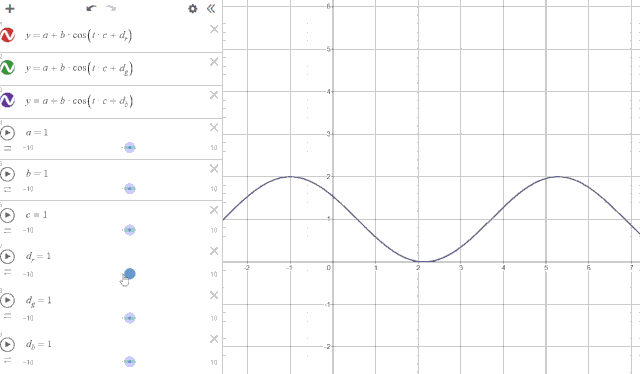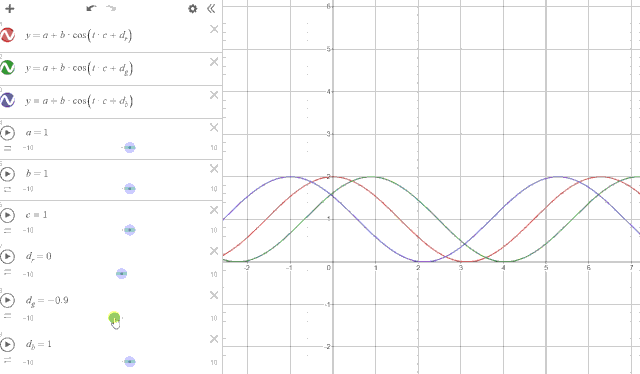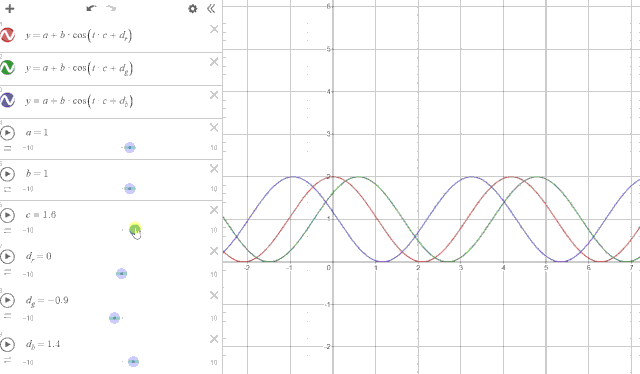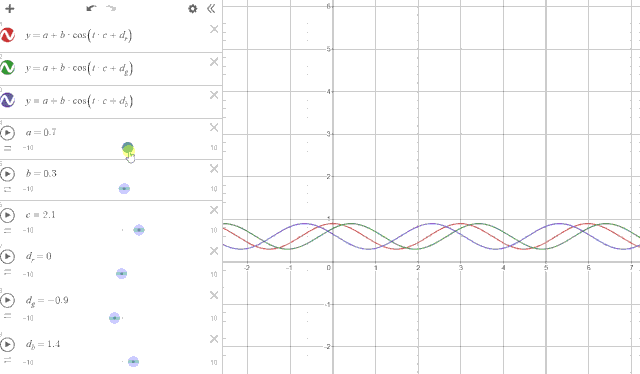
其中 t 区域是灰度的输入端,这里可以插入任意的灰度图。c 区域是权重值,控制输入灰度的变化区间。d 区是颜色变化的核心,这里设置个 float3,在每个分量上给不同的偏移值,这样颜色的 rgb 就会分离开(因为后面要做一次三角函数计算,这里相当于将每个 rgb 分量在 x 轴上进行偏移)。随后将偏移值和原始灰度相加,送去做 cosine 的操作(ue4 内部的 cos 自动在计算的时候帮你乘了 π,所以输入 2 就相当于输入了 2π,随后的 b 和 a 区域就是重映射的功能,乘 0.5 加 0.5 的操作将原始(-1,1)区间映射到(0,1)区间。
如果看到这里还是不理解,我做了张动图,对着下图看上面的参数应该就好懂了,其中红绿蓝三种颜色的曲线就代表了颜色中的 rgb,x 轴代表渐变横轴的位置,y 轴就是颜色的亮度。
其实这套做法并不是我的原创,早在 1999 年 Inigo Quilez 大佬就在他个人网站上放出了一套色板的计算方法。上面我所描述的算法就是他在博客中的这条公式:
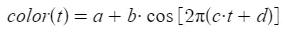
其中的所有字母变量都可以在上文找到对应讲解。这时你可能会问:这样控制一点都不直观,要怎样才能得到我想要的渐变效果呢?
对此 Inigo Quilez 放出了一套参数效果的对照表,如果你需要其中的某种渐变效果,只需要将每个值对应抄进去就好了(很简单是不是)。

二、使用对数函数平滑插值
有了上述色阶映射公式,对应 第二章 中分形的实现讲解,我们映射出来的结果是这样的(这里根据分形复变函数的 z 值映射色阶上的不同颜色。):

可以看到映射的结果不算好看,边缘有一圈圈的效果,我们希望映射出来的结果是下图所示的样子,边缘有非常平滑的过渡:

这要如何实现呢?Inigo Quilez大佬同样给出了他的解决方案,接下来我就以我的理解给大家讲解如何从“磨平”这些棱角,给边缘一个平滑的过渡。
我们都知道分形的计算来源于复变函数的不断迭代,对于曼德勃罗集合和朱利亚集合来说这个复变函数就是咱们之前提到的 z = z² + c ,同时为了避免某些数在迭代的过程中指数爆炸,我们设定了一个值 B 来限制迭代后 z 的值(提前说一下维数为2的曼德勃罗集合B为2,但是在计算平滑插值的时候我们可以把B设置的稍微大一点,比如50都是没问题的),如果 z 在迭代后的结果大于 B,那么我们认为当前迭代的这个点“逃逸”出去了,也代表这个点的迭代过程结束(即不参与下一次迭代)。
知道这些概念后,我们一起来看看,在有了 B 值的限制后,z 值的分布如下图所示(为了方便观察将结果压缩到了 0 - 1,压缩方法直接用 z 除区间最大值 B² 即可,为什么后面会讲):
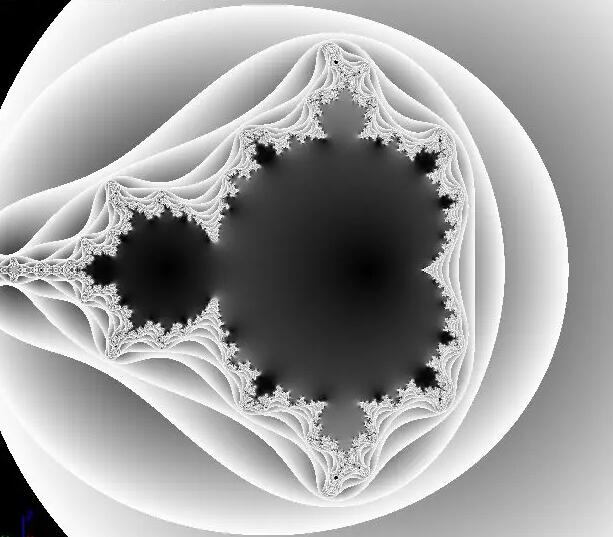
这里你可能会有点费解:为什么有一圈圈的渐变纹路?其实是因为最大值 B 限制的原因,这里我们一起来捋捋:
首先我把所有用到的字母变量都统一在这里解释一遍,方便理解:
z :复变函数迭代的主体 ,起始值为 0,随后不断迭代
d :分形函数的维度数 ,是一个 固定值 ,比如上面的图像维度为 2,d=2
c :是一个复数 ,参与每次迭代,为 固定值
B :最大值 ,如果某个点的z在迭代之后超过这个最大值,则迭代结束
首先我有一张复平面,上面分布着不同的复数,为了方便计算和理解,我们只取实轴上的点做计算。这时我们将复平面上的点代入复变函数 z = z²+c ,然后根据 B(限制最大值)的范围来判断当前的z是否超过了 B 的范围。如果超过了就停止计算这个点的迭代。

所以每次迭代 z 都会有一部分点超过了 B 值,这些点有些会超过非常多,有些可能是刚刚超过 B 一丢丢。所以我们可以得知,在每次被“淘汰”的点中是存在一个范围的,这时我们就需要去了解每一次迭代中被淘汰的z的范围是多少了。
刚刚我们说过每次迭代中超过 B 的范围可以是非常多,也可以是刚好超过 B 一丢丢,那么我们就可以得到每次“淘汰”出局的点的 z 的最小值应该是无限接近 B ,但是最大值是多少呢??如果仅仅在这个循环中想是非常难想的,所以我们应该换个思路,绕到上一次循环中寻找答案!!既然我们已经知道“淘汰”出局点的最小值是 B 了,那么在上一次循环中B也应该是最小值,因为循环之间是无缝衔接的,所以我们认定上一次循环的 z 的最小值也应该是下一次循环的最大值,如果我们设 z = z² + c 中的平方为 d ,那么 z 的最大值就应该是B的d次方,写成 B^d(因为指数出来的结果非常大,相比于此 c 的影响我们就忽略不计了)。

或许你看到这里会有点懵,我理解,因为我看这个算法的前5次也都是一脸懵逼的状态。理清楚关系,坚持看下去你一定可以看懂的,相信自己!
好的我们现在已经知道每个循环中 z 的最小值是 B ,最大值是 B^d,所以接下来要做的操作其实非常简单了,首先我们需要将 z 属于(B,B^d)的区间映射到(0,1)。怎么做呢,首先可以看到这个区间的数呈指数变化,并不是线性的,所以第一步我们可以用对数函数拿到他们的指数作为映射区间,指数变化摇身一变成了线性变换,公式如下:
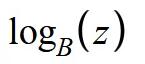
理解起来很简单,首先 z 是属于(B,B^d)的区间,这样运算的结果会将原本区间映射到(1,d)区间。但是我们需要(0,1)区间,所以我们还需要用 d 去做一次对数计算,和上面的加起来,公式应该是这样的:
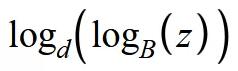
但是一般 shader 中自带的 log 函数是以 2 或者 10 为底数的,所以我们需要稍微修改一下这个公式的写法好让我们写入 shader。
首先我们根据这个公式:
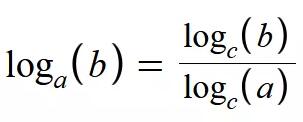
代入上面公式得到:
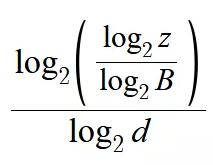
当当,成功了,这就是我们的映射公式!!顺带一提,这里你用 log2 或者用 ln 都是没问题的,因为底数不影响结果。
这时我们就得到了一份线性映射到 0-1 的 z 值图像。
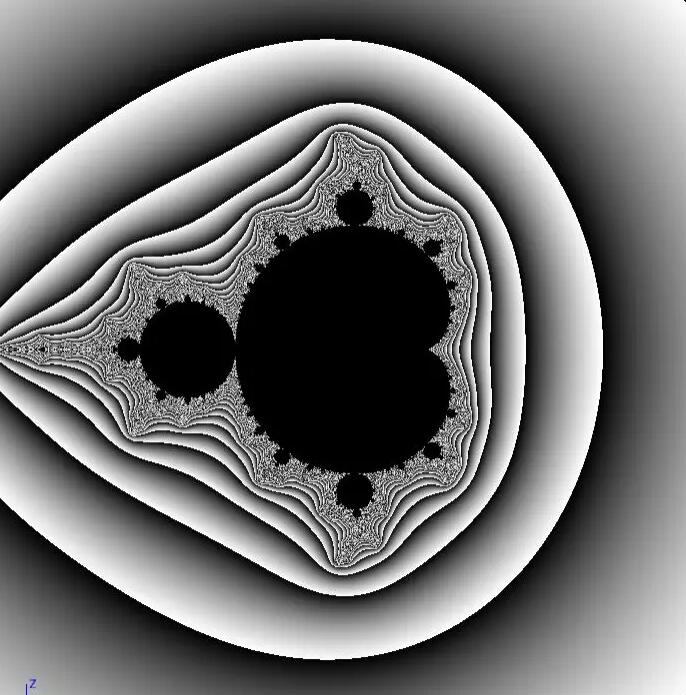
(如果你要问为什么要这么麻烦去搞什么对数函数,不直接把 z 减个啥数再除一下就压缩回去了嘛,我只能说你这样是转不成线性变换的,为什么一定要纠结线性变换,因为最后每个环之间都要首尾衔接!!!不是线性变换衔接后的结果会非常不平滑,请自动脑补 5 个 s 形首尾相接的结果。)
此时映射到 0-1 的函数图像是类似这样的(我统一了间距方便理解,实际上间距是不相等的,左边间距会小右边间距会很长,看上面图片也能很直观的感受到,所以不要在此处纠结太多)
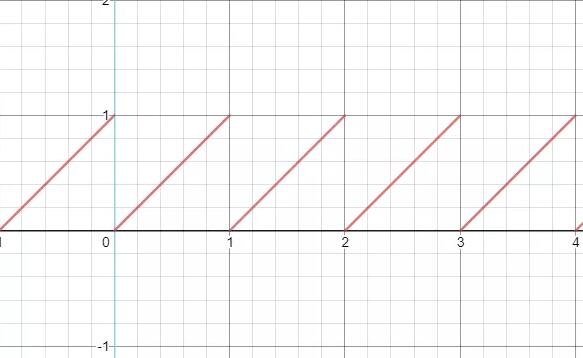
接下来我们只需要用每次迭代被“淘汰”部分点所迭代的次数(下图蓝色线部分)加上(减去其实效果也差不多,只是画面亮度会整体偏移一个单位)上面算好的区间,就可以得到下图中的绿线。当然分形的迭代范围宽度是从左到右越来越窄的,所以这条绿线实际显示更像是一条抛物线。
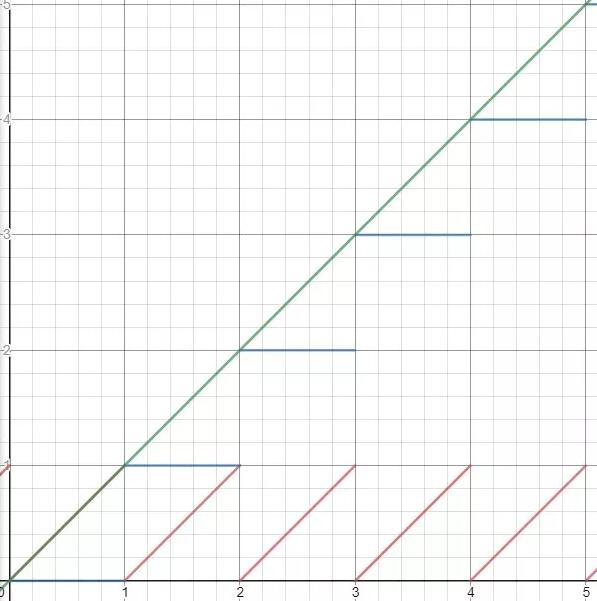
做到这里,我们基本上已经完美解决平滑过渡的问题了。运用输出的结果如下(这里为了方便观察画面还需要做一步范围映射的操作,也就是需要用最后结果除以最大的循环次数):

接下来的工作就简单了,我们只需要将这个灰度应用上面讲到的范围映射就可以得到很漂亮的分形效果!

三、代码实现
完整节点和代码如下所示:
// 统一定义一些必要的变量
float xnew , ynew , n=0 , B = 60 , sit ;
float3 tmp;
float2 znew, z = (0,0);
// 将屏幕uv空间缩放至原来的两倍并将0点挪到屏幕中心
C = C * 4 - 2;
// 复变函数循环开始
for(int i = 0; i<times; i++)
{
z = float2(
cos( atan(z.y/z.x)*d)*pow(length(z),d),
sin( atan(z.y/z.x)*d)*pow(length(z),d)
)+C;
if(dot(z,z)>B*B)break;
// 循环次数加一(每个层级不一样)
n += 1;
}
// 将z的区间映射到0-1,然后和循环次数相减得到平滑的过渡
sit =n - log2(log2(length(z))/(log2(B)))/log2(d);
//将映射结果运用颜色映射
tmp = 0.5 + 0.5*cos( 3.0 + sit*0.075*d + float3(0.0,0.6,1.0));
return tmp;
终于讲完啦,神奇的数学,总能带给我们惊喜!
研究这章耗费的时间确实挺多的,好在多次尝试后终于弄懂了,那种成就感真的特别强!也希望通过这几章的讲解能让你爱上分形,爱上数学,同样也爱上解决问题的思考过程。
欢迎关注“包小猩CG杂货店”微信公号
